[BOJ]2225번: 합분해(c++)

https://www.acmicpc.net/problem/2225

2225번: 합분해

 

#include <iostream>
 
using namespace std;
 
int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
 
    const int MAX = 200;
    const int mod = 1000000000;
    // 2개 이상의 요소를 더하면서 오버플로가 발생할 수 있으므로, long long 형으로 선언
    long long D[MAX + 1][MAX + 1] = { 1, };
    
    int N, K;
    cin >> N >> K;
    
    /*
        D[K][N] : 0 ~ N까지의 정수 K개를 더해서 그 합이 N이 되는 경우의 수
    
        N = (K-1 개의 수) + L  (이때, 0 <= L <= N )
 
        --> 점화식 : D[K][N] = Sum(D[K - 1][N - L])
    */
    for (int i = 1; i <= K; i++)
    {
        for (int j = 0; j <= N; j++)
        {
            for (int l = 0; l <= j; l++)
            {
                D[i][j] += D[i - 1][j - l];
                D[i][j] %= mod;
            }
        }
    }
 
    cout << D[K][N];
 
    return 0;
}

 

java소스로 된 풀이도 있지만...

이번에 c++로 다시 풀어보면서 좀더 DP스럽게 풀이해보았다. 

백준님의 강의 자료를 많이 참고하였다 ㅠㅠ

 

 

0부터 N까지의 정수 K개를 더해서 그 합이 N이 되는 경우의 수를 구하는 프로그램을 작성하시오.
덧셈의 순서가 바뀐 경우는 다른 경우로 센다(1+2와 2+1은 서로 다른 경우). 또한 한 개의 수를 여러 번 쓸 수도 있다.

 

1. 덧셈의 순서가 바뀐 경우도 카운팅 하는 점

2. 한 개의 수를 여러번 쓸 수 있는 점

때문에 이 문제는 DP문제이다. 

 

D[K][N],  0 ~ N까지의 정수 K개를 더해서 그 합이 N이 되는 경우의 수를 구하기 위해서는

더 작은 규모의 문제로 쪼개서 작은 단위부터 구해야 한다. 

 

N에 더해진 마지막 숫자 L을 제외하면, 나머지는 K -1개의 수로 더해진 N - L이다.

 

N을 구성하는 K개의 숫자가 있고, 마지막으로 L을 더한다고 생각하자.

그렇다면 L을 제외한 나머지 숫자의 개수는 K - 1 개 이고, 그 합은 N - L 이다.

 

 

D[K][N]의 경우의 수는 D[K-1][N-L]이다. 숫자 L은 무시한다. 경우의 수를 구하므로

 

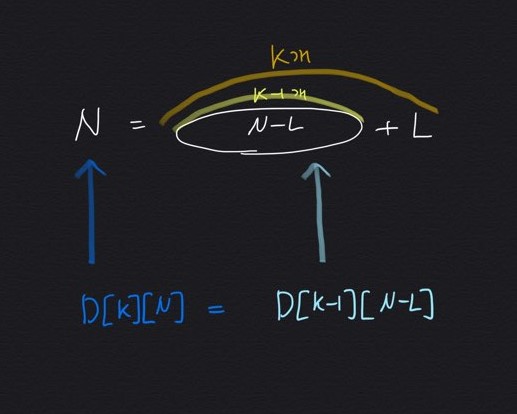
우리는 경우의 수를 구하는 것이므로,

D[K][N] = D[K - 1][N - L] 이라고 대략 생각할 수 있다.  

 

 

문제에서 L, 즉 개개의 숫자는 0 ~ N 의 범위에 있다.

 

그런데 이때, L의 범위가 0 이상 N이하 라는 것을 생각하면

 

 

 

따라서 D[K][N] 는 결국 D[K - 1][0 ~ N] 의 합이다. 

 

바텀업으로 풀이하는 것이 생각하는 과정과 제일 유사하다.