https://www.acmicpc.net/problem/2225
2225번: 합분해
첫째 줄에 답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
정확히는 (방법1까지는) 더 쉬운! 풀이이다 ㅋㅋ
합분해 문제 1편 참고
소스 먼저, 설명은 아래에
방법 1: 그림을 그려서 더 직관적으로 풀기. O(KN)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
#include <iostream>
using namespace std;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
const int MAX = 200;
const int mod = 1000000000;
long long D[MAX + 1][MAX + 1] = { 1, };
int N, K;
cin >> N >> K;
/*
점화식
D[K][N] : 0 ~ N까지의 정수 K개를 더해서 그 합이 N이 되는 경우의 수
N = (K-1 개의 수) + L (이때, 0 <= L <= N )
D[K][N] = (D[K - 1][0] + ... + D[K - 1][N - 1]) + D[K - 1][N]
= D[K][N - 1] + D[K - 1][N]
--> D[K][N] = D[K][N - 1] + D[K - 1][N]
*/
for (int i = 1; i <= K; i++)
{
D[i][0] = 1;
for (int j = 1; j <= N; j++)
{
D[i][j] = (D[i][j - 1] + D[i - 1][j]) % mod;
}
}
cout << D[K][N];
return 0;
}
Colored by Color Scripter
|
방법 2: 한단계 더 나아가자. 1차원 다이나믹 O(KN)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
#include <iostream>
using namespace std;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
const int MAX = 200;
const int mod = 1000000000;
long long S[MAX + 1] = { 1,};
int N, K;
cin >> N >> K;
/*
점화식
D[K][N] : 0 ~ N까지의 정수 K개를 더해서 그 합이 N이 되는 경우의 수
D[K][N] = D[K - 1][N] + D[K][N - 1]
S[N] : D[K][N] 이라 하면
S[N] = k번 sum(S[N] + S[N - 1])
*/
for (int i = 1; i <= K; i++)
{
for (int j = 1; j <= N; j++)
{
S[j] += S[j - 1];
S[j] %= mod;
}
}
cout << S[N];
return 0;
}
Colored by Color Scripter
|
역시 백준님 강의자료를 많이 참고하였다.
글로는 도저히 설명할 자신이 없어서 그림을 그려왔다.
TIP1
숫자가 현란하다 싶으면 그림을 그려보자
먼저 방법 1.
숫자가 더해지는 과정을 N*K 사각형으로 그리면 다음과 같다.

이 수를 보다보면 느낌이 좀 오는데...

그림으로 그리니 이렇게 쉬울수가 ㅜㅜ
저걸 그대로 구현한 것이 방법1 풀이이다.
합분해 첫번째 풀이에서 골치썩히던게 매우 억울하다
여기서 만족하고 싶었지만, 다음 풀이로 더 넘어가보자.
TIP2
내가 간과하던 규칙이 있을 수 있다.
위의 그림을 다시 불러와보자.
이 네모 칸 안에 숫자를 써넣을때,
우리는 분명 숫자를 위에서 아래로, 왼쪽에서 오른쪽으로 더하면서 써내려갔다.

여기서 한번만 생각의 점프를 해보면
D[K - 1][N]은 1회차 전의 D[K][N]라고 생각할 수 있지 않을까?!
위에서 아래로 <-- 를 for문으로 바꿔보자
그리고 i = 1일때 숫자를 한번 써보면..

i = 2일때 숫자도 한번 써보면..

감이 좀 왔겠지만,
i 회차의 한 사각형 값은
i - 1회차의 같은 자리 값 + i회차의 왼쪽 값과 같다.
이제 새로운 점화식 S[N] (= D[K][N]) 으로 나타내보자

i회차의 S[N] = i - 1회차의 S[N] + i회차의 S[N - 1]
이라는 점화식 완성!
간단하게 수도코딩을 해보면 다음과 같다.

당연하게도 합분해 첫번째 포스팅 풀이 O(KN^2) 보다는
이번 포스팅의 방법1 O(KN)이 빠르고,
방법1 풀이 보다는 방법2가 공간 점유율이 낮다.
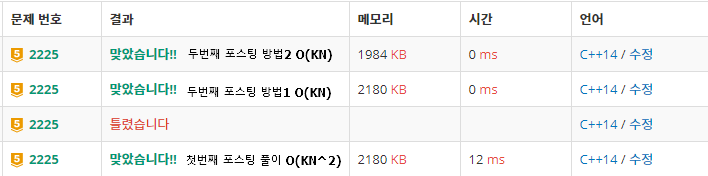
다 쓰고나니 별거 아닌것처럼 보이는데...ㅋㅋㅋㅋ
나에겐 벽 하나나 마찬가지였으니, 누군가에게도 도움이 되길!
'Algorithm > BOJ' 카테고리의 다른 글
| [BOJ]1107번: 리모컨(c++) (0) | 2020.05.03 |
|---|---|
| [BOJ]3085번: 사탕 게임(c++) (0) | 2020.05.02 |
| [BOJ]17404번: RGB거리 2(c++) (0) | 2020.04.27 |
| [BOJ]11656번: 접미사 배열(c++) (0) | 2020.04.25 |
| [BOJ]11655번: ROT13(c++) (0) | 2020.04.25 |
댓글