https://www.acmicpc.net/problem/1967
1967번: 트리의 지름
파일의 첫 번째 줄은 노드의 개수 n(1 ≤ n ≤ 10,000)이다. 둘째 줄부터 n번째 줄까지 각 간선에 대한 정보가 들어온다. 간선에 대한 정보는 세 개의 정수로 이루어져 있다. 첫 번째 정수는 간선이 ��
www.acmicpc.net
postorder로 깊이우선 탐색. 서브트리의 양 가지 끝을 탐색하여 그 가중치 값을 더한 것중의 최대값을 구한다
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct node {
int to, weight;
};
struct path {
int cost, max_cost;
};
// postorder로 깊이우선 탐색
path dfs(vector<vector<node>> &tree, vector<bool> &visit, int now)
{
visit[now] = true;
// 지나온 경로들의 가중치를 저장할 벡터
vector<int> branch;
// 모든 dfs함수를 지나며 얻어지는 가중치합 중의 최대값을 담게 된다.
int cost_sum = 0;
// 연결된 노드 탐색 (탐색 대상이 자식 노드가 아닐수 있다)
for (node c : tree[now])
{
if (!visit[c.to])
{
// dfs재귀함수 호출 결과 : 지나온 경로
path past = dfs(tree, visit, c.to);
// (이전 노드 시점의 가중치합 + 현재 노드~이전 노드 사이의 가중치) -> branch push
branch.push_back(past.cost + c.weight);
// 전 경로 통틀어서 가중치합 최대값 갱신
cost_sum = max(past.max_cost, cost_sum);
}
}
// 내림차순 정렬
sort(branch.begin(), branch.end(), [](const int &a, const int &b) ->bool{
return a > b;
});
int cost = 0;
// 현재 노드에 연결된 노드가 1개 이상이면
if (branch.size() >= 1)
{
// 현재 노드 시점에서의 최대 가중치 합
cost = branch[0];
cost_sum = max(cost, cost_sum);
}
/*
현재 노드에 연결된 노드가 2개 이상이면
현재 노드는 지름의 중간에 위치한 상황.
--> 최대 가중치 합 = 한쪽 서브트리의 가중치합 + 다른 한쪽 서브트리의 가중치합
*/
if (branch.size() >= 2)
{
cost_sum = max(branch[0] + branch[1], cost_sum);
}
return {cost, cost_sum};
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// 입력
int N;
cin >> N;
vector<vector<node>> tree(N + 1, vector<node>());
for (int i = 0; i < N - 1; ++i)
{
int from, to, weight;
cin >> from >> to >> weight;
tree[from].push_back({ to, weight});
tree[to].push_back({ from, weight});
}
// 임의 노드에서부터 postorder 깊이우선 탐색으로 최대 지름(가중치 합) 구하기
vector<bool> visit(N + 1);
path p = dfs(tree, visit, 1);
// 출력
cout << p.max_cost;
return 0;
}
1167번 트리의 지름과 같은 문제이다.
해당 링크에 있는 소스코드를 입력부분만 살짝 수정해서 돌려도 돌아간다!
그래서 이번엔 다른코드로 짜보았다. 순서는 다음과 같다.
1. postorder 탐색으로, 한 노드에 연결된 서브트리를 탐색한다.
2. 각 서브트리의 최대 가중치 합을 구한다
3. --> 전체 트리의 최대 가중치합이 구해진다.
말로는 조금 복잡해서... 또다시 등장한 그림!
헷갈리지 않도록 노드를 알파벳으로 표기하였다.
역시 아무노드에서부터 시작해도 된다.

post order 이므로, 말단 노드에서부터 가중치 합을 구하게 된다.
말단에서의 가중치합은 당연히 0이다.
이 아래서부터 약간 헷갈리기 시작할건데...
cost는 해당 노드시점에서의 최대 가중치고,
max는 해당 노드가 양 서브트리의 중간에 있을 경우, 그 지름의 크기이다.

D와 E는 C에서 만나게 된다.
이때, 각 경로가 반환한 가중치값 + 현재노드~직전 노드 가중치 를 각각 계산한다.
// (이전 노드 시점의 가중치합 + 현재 노드~이전 노드 사이의 가중치) -> branch push
branch.push_back(past.cost + c.weight);그리고 이 값들 중 가장 큰 값 6이 노드 C 시점에서의 가중치 합이다.
그리고 만약 C - D - E가 지름일 경우, 그 값은 10 이다.

노드 C는 B에서 자신의 가중치합 6, 지름값 10을 반환한다.
C의 반환값 6 + B~C의 가중치 3 = 9가 B의 가중치 합이다.
그런데 이때, D - C - B가 지름이라고 해도 9는 기존의 max 10보다 작다.
따라서 max는 그대로 10이다.
// 현재 노드에 연결된 노드가 1개 이상이면
if (branch.size() >= 1)
{
// 현재 노드 시점에서의 가중치 합
cost = branch[0];
cost_sum = max(cost, cost_sum);
}
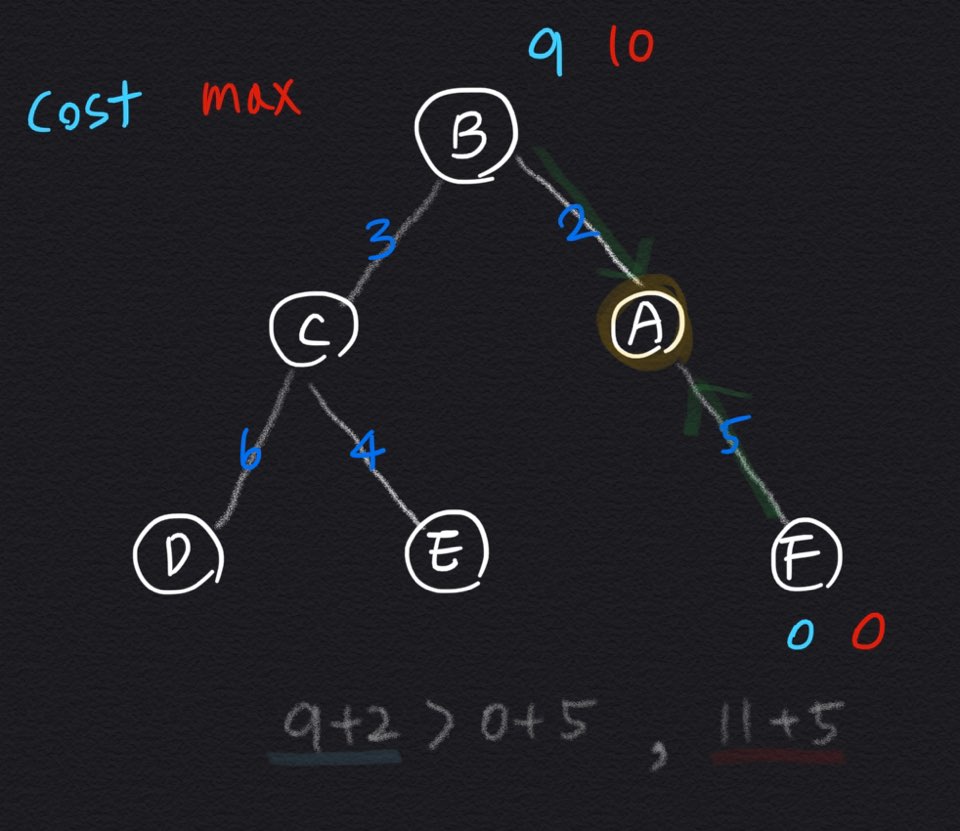
마찬가지로 각 경로가 반환한 가중치값 + 현재노드~직전 노드 가중치 를 각각 계산한다.
그러면 A에서 cost는 11,
max는 D - C - B - A - F가 지름일 경우 11 + 5 = 16이 된다.
/*
현재 노드에 연결된 노드가 2개 이상이면
현재 노드는 지름의 중간에 위치한 상황.
--> 지름 = 한쪽 서브트리의 가중치합 + 다른 한쪽 서브트리의 가중치합
*/
if (branch.size() >= 2)
{
cost_sum = max(branch[0] + branch[1], cost_sum);
}
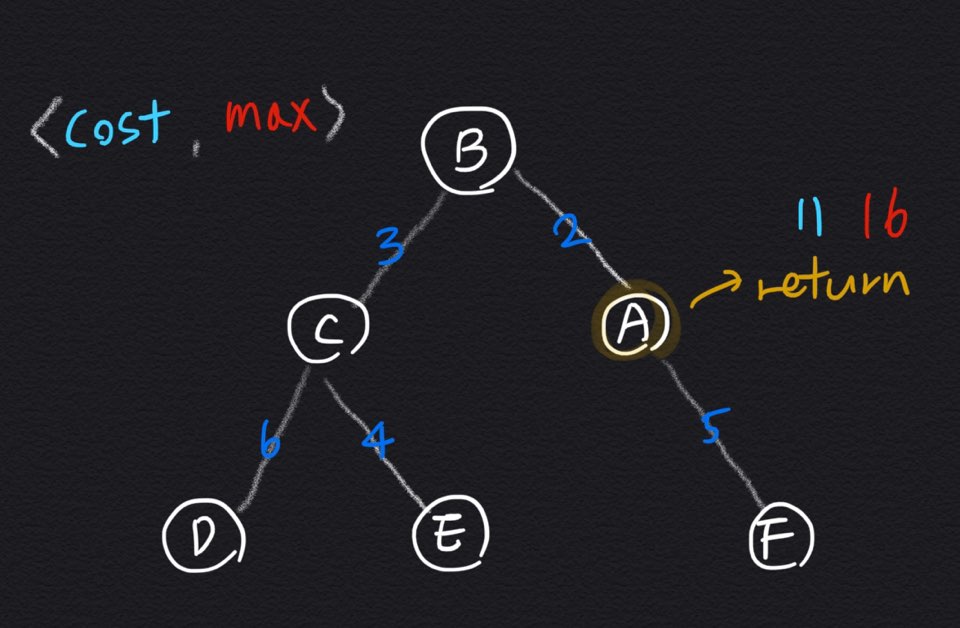
결국 max는 전 노드를 탐색하며 얻어진 최대 지름값이 된다
끝!
그림 그리는것도 어렵구만
'Algorithm > BOJ' 카테고리의 다른 글
| [BOJ]14888번: 연산자 끼워넣기 (c++) (0) | 2020.06.02 |
|---|---|
| [BOJ]1339번: 단어 수학 (c++) (0) | 2020.06.02 |
| [BOJ]1167번 : 트리의 지름 (c++) (0) | 2020.05.31 |
| [BOJ]11725번 : 트리의 부모 찾기 (c++) (0) | 2020.05.31 |
| [BOJ] 2250번: 트리의 높이와 너비 (c++) (0) | 2020.05.31 |

댓글