https://programmers.co.kr/learn/courses/30/lessons/42861
코딩테스트 연습 - 섬 연결하기
4 [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] 4
programmers.co.kr
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
// 노드x가 포함된 트리의 루트노드 가져오기
int get_root(vector<int> &parent, int x)
{
// x가 노드x의 부모라면
if (x == parent[x])
{
return x;
}
/*
다른 노드가 노드x의 부모라면,
루트노드를 찾을 때까지 재귀함수 호출.
마지막에 노드x의 부모에 해당 루트노드 저장후 반환
*/
return parent[x] = get_root(parent, parent[x]);
}
// 트리 합치기
void union_parent(vector<int>& parent, int a, int b)
{
/*
두 노드 a, b가 포함된 트리의 루트노드 숫자를 비교하여
더 적은 숫자의 루트노드 트리로 편입
*/
a = get_root(parent, a);
b = get_root(parent, b);
if (a < b)
{
parent[b] = a;
}
else
{
parent[a] = b;
}
}
// 서로 동일한 트리에 포함되어 있는지 여부 확인
bool find_parent(vector<int>& parent, int a, int b)
{
a = get_root(parent, a);
b = get_root(parent, b);
return (a == b);
}
int solution(int n, vector<vector<int>> costs) {
// costs : [from, to, cost]순으로 저장된 2차원 벡터
// 비용을 기준으로 오름차순 정렬
sort(costs.begin(), costs.end()
, [&costs](vector<int> &a, vector<int> &b)
{
return a[2] < b[2];
}
);
// 모든 노드의 부모를 자기자신으로 초기 세팅
vector<int> parent(n);
for (int i = 0; i < n; ++i)
{
parent[i] = i;
}
// 최소비용으로 모든 섬을 연결하는 다리 건설하기
int sum = 0;
for (int i = 0; i < costs.size(); ++i)
{
// 두 노드의 소속 트리가 다르다면
if (!find_parent(parent, costs[i][0], costs[i][1]))
{
// 다리 건설
sum += costs[i][2];
// 한쪽 트리로 편입시키기
union_parent(parent, costs[i][0], costs[i][1]);
}
}
return sum;
}
union-find 알고리즘과 크루스칼 알고리즘을 아직 모른다면??
나동빈님 블로그에서 먼저 공부를 하는 것이 최대효용을 증가시킬 수 있습니다,,
https://blog.naver.com/ndb796/221230967614
17. Union-Find(합집합 찾기)
Union-Find(유니온-파인드)는 대표적인 그래프 알고리즘입니다. 바로 '합집합 찾기'라는 의미를 가진 알...
blog.naver.com
https://blog.naver.com/ndb796/221230994142
18. 크루스칼 알고리즘(Kruskal Algorithm)
이번 시간에 다루어 볼 내용은 바로 크루스칼 알고리즘입니다. 크루스칼 알고리즘은 가장 적은 비용으로 모...
blog.naver.com
알고리즘 문제해결 전략 종만북 을 봐도 이해가 쉽사리 안되던게
나동빈님 블로그 & 유튜브 강의를 보고 한번에 이해가 됐다.
TIP_이 문제에서 크루스칼 알고리즘을 사용해야 하는 이유
1. 문제 요구사항
최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.
다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다.
A. 최소의 비용으로
B. 모든 노드가 이어진
C. 사이클이 발생하지 않는 트리를 만들어야 하기 때문이다.
이를 MST (Minimum Spanning Tree, 최소 신장트리)라고 한다.
2. 문제 조건 - 간선의 밀집도
섬의 개수 n은 1 이상 100 이하입니다.
costs의 길이는 ((n-1) * n) / 2이하입니다.
사실 MST를 만드는 알고리즘은 두개가 있다.
크루스칼 알고리즘과 프림 알고리즘인데,
크루스칼은 간선을 기준으로 선택해나가고, 프림은 노드를 기준으로 선택해 나간다.
따라서 이 문제처럼 그래프가 적은 간선을 가지는 희소 그래프라면 크루스칼 알고리즘이 적합하다.
더 자세한 사항은 다음 블로그 참조
https://gmlwjd9405.github.io/2018/08/30/algorithm-prim-mst.html
[알고리즘] Prim 알고리즘 이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
좋아 그럼 크루스칼은 알겠어. 근데 Union-Find 알고리즘은 왜?
냐고 물으신다면 대답해드리는게,, 흠흠
크루스칼 알고리즘의 기본 아이디어는 다음과 같다.
1. 적은 비용을 가지는 간선을 선택해 나가자. --> 선택 후엔 노드를 기준트리에 포함
2. 근데 해당 간선의 노드들이 이미 기준트리에 포함된 노드라면? 패스
여기서 저 기준트리라는 표현에 대해 의문이 생길 수 있다.
그거 그냥 bool벡터같은 걸로 선택 여부만 판단하면 안되나?
하지만 기준트리 판단 없이 단순히 노드의 선택여부만 판단한다면 다음과 같은 반례가 생긴다.
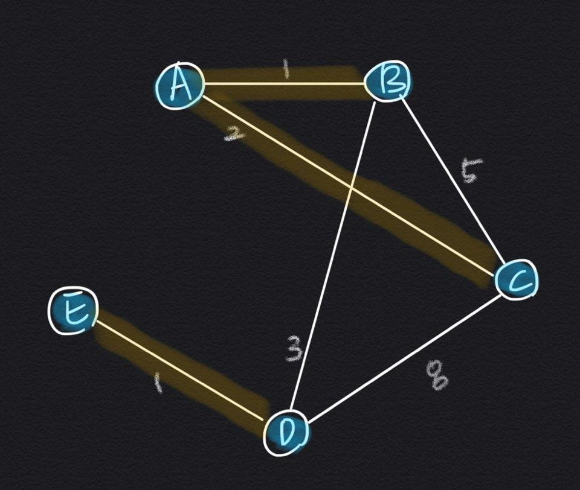
따라서
1. 비용을 기준으로 오름차순 정렬된 간선을 탐색해 나간다.
2. 소속이 다른 노드를 기준트리에 추가시켜 나간다.
3. 모든 노드가 동일한 기준트리에 포함될때까지!
// 최소비용으로 모든 섬을 연결하는 다리 건설하기
int sum = 0;
for (int i = 0; i < costs.size(); ++i)
{
// 두 노드의 소속 트리가 다르다면
if (!find_parent(parent, costs[i][0], costs[i][1]))
{
// 다리 건설
sum += costs[i][2];
// 한쪽 트리로 편입시키기
union_parent(parent, costs[i][0], costs[i][1]);
}
}
'Algorithm > 프로그래머스' 카테고리의 다른 글
| [프로그래머스]탐욕법(Greedy) : 저울 (level 3)(c++) (0) | 2020.06.19 |
|---|---|
| [프로그래머스]탐욕법(Greedy) : 단속카메라 (level 3)(c++) (0) | 2020.06.19 |
| [프로그래머스]동적계획법(Dynamic Programming) : 등굣길 (level 3)(c++) (0) | 2020.06.18 |
| [프로그래머스]동적계획법(Dynamic Programming) : 정수 삼각형 (level 3)(c++) (0) | 2020.06.17 |
| [프로그래머스]동적계획법(Dynamic Programming) : 타일 장식물 (level 3)(c++) (0) | 2020.06.16 |

댓글