https://www.acmicpc.net/problem/11729
11729번: 하노이 탑 이동 순서
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net
분할 정복
#include <iostream>
#include <vector>
using namespace std;
void move_tower(int N, int from, int to, int mid)
{
if (N == 0)
{
return;
}
// 1 ~ N -1 탑 이동 : from -> mid (to 경유)
move_tower(N - 1, from, mid, to);
// 마지막 원판 : from -> to 이동
cout << from << ' ' << to << '\n';
// 1 ~ N -1 탑 이동 : mid -> to (from 경유)
move_tower(N - 1, mid, to, from);
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// 입력
int N;
cin >> N;
// 원판 총 이동 횟수 출력
cout << (1 << N) - 1 << '\n';
// 하노이탑 이동 : 1번 -> 3번 (2번 경유)
move_tower(N, 1, 3, 2);
return 0;
}
고전적인 분할정복 문제이다.
그림을 그려서 파악하는 것이 더 쉽다.
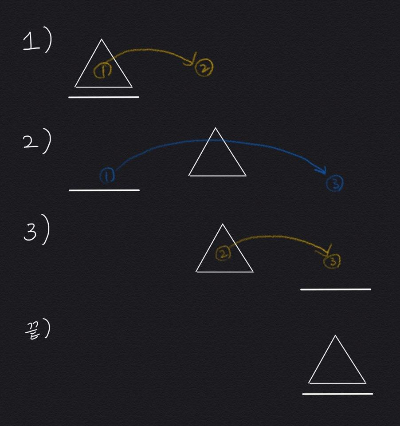
시작점을 from, 도착점을 to, 중간 경유지를 mid라고 했을 때
1. 1 ~ (N-1) 을 from -> mid로 옮긴다. (이 때, 중간 경유지는 to)
2. 마지막 원판 N을 from -> to로 옮긴다.
3. 1 ~ (N-1)을 다시 mid -> to로 옮긴다. (이 때, 중간 경유지는 from)
위 내용을 재귀함수로 구현하면 된다.
하노이 탑 이동횟수를 구하는 것은 점화식을 세워봐야 한다.
결과적으로 N개의 하노이탑을 옮기려면 2^N - 1번 이동해야 하는데
자세한 식은 아래에...
A[n]를 N개 하노이탑을 이동하는 총 횟수라고 하자.
그러면 위 내용을 식으로 쓰면
--> A[n] = A[n - 1] + 1 + A[n - 1]
--> A[n] = 2 * A[n - 1] + 1
양변에 1씩 더해주면
--> A[n] + 1 = 2 * A[n - 1] + 2
--> A[n] + 1 = 2 * (A[n - 1] + 1)
S[n]를 A[n] + 1이라 하면
--> S[n] = 2 * S[n - 1]
--> S[n] = 2 * 2 * S[n - 1]
...
--> S[n] = 2^(n - 1) * S[1]
이때 S[1] = A[1] + 1 = 1 + 1 = 2 이므로
--> S[n] = 2^(n - 1) * 2
--> S[n] = 2^n
S[n] = A[n] + 1이었으므로
--> A[n] + 1 = 2^n
--> A[n] = 2^n - 1
즉, N개 하노이탑을 이동하는 총 횟수는 2^n - 1이다!
'Algorithm > BOJ' 카테고리의 다른 글
| [BOJ]1981번: 배열에서 이동 (c++) (0) | 2020.07.16 |
|---|---|
| [BOJ]1939번: 중량제한 (c++) (0) | 2020.07.15 |
| [BOJ]1780번: 종이의 개수 (c++) (0) | 2020.07.08 |
| [BOJ]2110번: 공유기 설치 (c++) (0) | 2020.07.08 |
| [BOJ]2805번: 나무 자르기 (c++) (0) | 2020.07.08 |
댓글