https://www.acmicpc.net/problem/10972
10972번: 다음 순열
첫째 줄에 입력으로 주어진 순열의 다음에 오는 순열을 출력한다. 만약, 사전순으로 마지막에 오는 순열인 경우에는 -1을 출력한다.
www.acmicpc.net
시간복잡도 : O(N)
#include <iostream>
using namespace std;
bool next_permutation(int numbers[], int N)
{
// i : 뒤에서부터 시작 되는 가장 긴 증가 수열의 마지막 인덱스
int i = N - 1;
while (i > 0 && numbers[i - 1] > numbers[i])
{
--i;
}
// 전체가 내림차순인 상태 : 마지막 순열
if (i <= 0)
{
return false;
}
// j : i - 1 < j , A[i - 1] < A[j] 인 수.
// i번째 수 바로 앞의 수보다 큰 수 찾기
int j = N - 1;
while (numbers[i - 1] > numbers[j])
{
--j;
}
// i번째 수와 j번째 수를 바꾸기
swap(numbers[i - 1], numbers[j]);
// i 번째 수부터 마지막까지 모두 뒤집기
for (int k = i, h = N - 1; k < h; ++k, --h)
{
swap(numbers[k], numbers[h]);
}
return true;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
const int MAX = 10000;
int numbers[MAX];
// 입력
int N;
cin >> N;
for (int i = 0; i < N; ++i)
{
cin >> numbers[i];
}
// 다음 순열이 존재하면 출력
if (next_permutation(numbers, N))
{
for (int i = 0; i < N; ++i)
{
cout << numbers[i] << ' ';
}
cout << '\n';
}
// 존재하지 않으면 -1 출력
else
{
cout << -1;
}
return 0;
}
처음에는 완전 브루트 포스로 풀었다.
전체 순열을 만들어서 문제에서 주어진 값을 찾으면,
그다음 순열을 출력하는 식으로 하다가 시간초과!
그렇게 되면 시간 복잡도가 O(N! * N) 가 되어버리기 때문이다
= 전체 수열 구하기 O(N!) * 각각의 경우에서 주어진 순열과 일치하는지 검사 O(N)
따라서 저 문제는, 사전 순 정렬의 원리를 그대로 구현해야 한다.
코드는 백준님의 강의 자료를 많이 참고하였다 ㅜㅜ
예를 들어 1 2 5 4 3 이라는 수열이 주어졌을 때,
우리는 어떻게 다음 사전식 순열을 찾을 수 있는가?

1 2 3 4 5 처럼 모든 수가 A[i - 1] < A[i]라면 5는 수상하지 않았을 것이다.
사전식 순열은 수를 뒤에서부터 바꾸어 나가므로,
먼저 뒤에서부터 이어진 증가순열의 끝( = 5)을 찾는다.
그리고 그 앞의 2는 이제 할일이 있다.
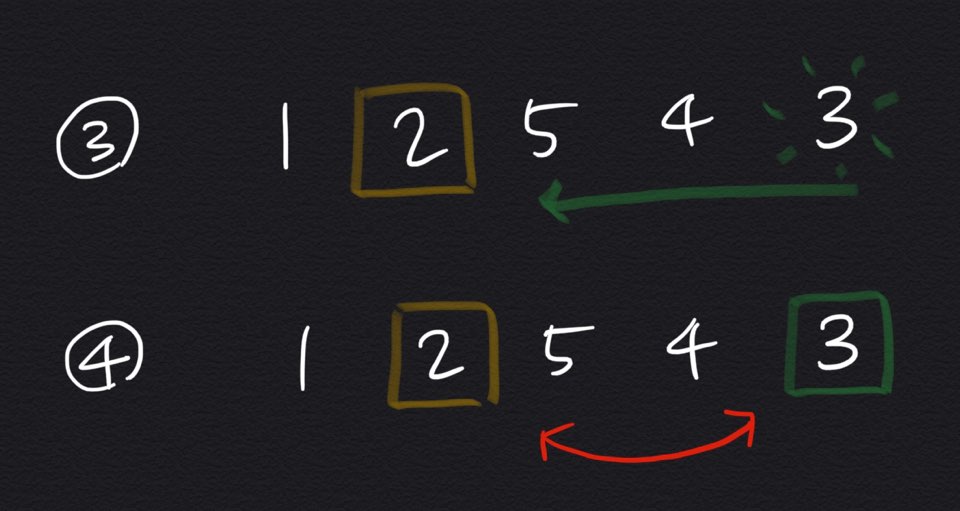
먼저 2의 뒤에 있는 수 중에서, 뒤에서부터 2보다 큰 수를 찾는다.
그리고 그 수와 자리를 바꾼다.

짠! 이제 이 순 열은 1 2 _ _ _ 가 아니라, 1 3 _ _ _ 의 텀이 되었다.
그리고 그 뒤의 숫자들은 앞뒤를 모두 바꾸어준다.
그러면 다음 사전식 순열 완성!
물론 내가 이 규칙을 발견하고 쓴 글이 아니고,,
내가 무의식적으로 사전순 정렬하던 것에는 이러한 순서가 있었는가,,
매우 신기하다.
'Algorithm > BOJ' 카테고리의 다른 글
| [BOJ]10974번: 모든 순열(c++) (0) | 2020.05.11 |
|---|---|
| [BOJ]10973번: 이전 순열(c++) (0) | 2020.05.11 |
| [BOJ]15666번: N과 M (12)(c++) (0) | 2020.05.10 |
| [BOJ]15665번: N과 M (11)(c++) (0) | 2020.05.09 |
| [BOJ]15664번: N과 M (10)(c++) (0) | 2020.05.09 |
댓글