https://www.acmicpc.net/problem/1201
1201번: NMK
1부터 N까지의 수를 한 번씩 이용해서 최대 부분 증가 수열의 길이가 M이고, 최대 부분 감소 수열의 길이가 K인 수열을 출력한다.
www.acmicpc.net
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// 입력
int N, M, K;
cin >> N >> M >> K;
/*
정답이 없는 경우
1. 최대 부분 증가수열과 최대 부분 감소 수열은 하나의 원소만 공유한다.
2. 비둘기집 원리
: N = M * K + 1이면 길이가 M + 1인 증가수열 또는 길이가 K + 1인 감소 수열을 만들 수 있다.
*/
if (N < M + K - 1 || N > M * K)
{
cout << -1;
return 0;
}
vector<int> nums(N);
for (int i = 0; i < N; ++i)
{
nums[i] = i = 1;
}
/*
ex) N = 8, M = 4, K = 3 이면 --> (1)(3 2)(5 4)(8 7 6) 형태로
최대 길이 K의 그룹 M개로 나누어 그 안에서 뒤집어준다.
*/
int g_strt = 0;
for (int i = 1; i <= M; ++i)
{
// 각 그룹은 최소 1개, 최대 K개 요소를 가질 수 있다.
int g_end = min(g_strt + K, N - M + i);
// [g_strt, g_end)의 요소들을 뒤집기
reverse(nums.begin() + g_strt, nums.begin() + g_end);
// 다음 그룹 시작은 g_end부터
g_strt = g_end;
}
// 출력
for (int i = 0; i < N; ++i)
{
cout << nums[i];
}
return 0;
}
1부터 N까지의 수를 한 번씩 이용해서 최대 부분 증가 수열의 길이가 M이고,
최대 부분 감소 수열의 길이가 K인 수열을 출력한다.
불가능한 경우의 조건을 찾는 것이 어려워서 많이 찾아봤다.
1. N의 최소조건 (N >= M + K - 1)
- 최대 부분 증가수열과 최대 부분 감소 수열은 하나의 원소만 공유한다.
가장 긴 바이토닉 수열 문제 풀이에 멋진 그림이 있다... (아래쪽에도 있다)
2. N의 최대조건 (N <= M * K)
- N은 최대 길이가 K개인 그룹 M개로 나눌수 있다.
- N = M * K + 1이면 길이가 M + 1인 증가수열 또는 길이가 K + 1인 감소 수열을 만들 수 있다.
비둘기집의 원리를 알아두자.
이 문제의 기본 전략은 다음과 같다
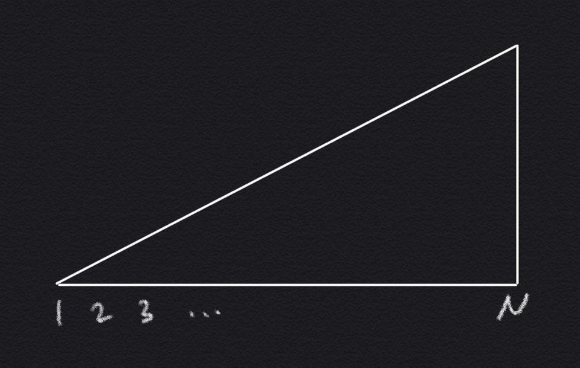
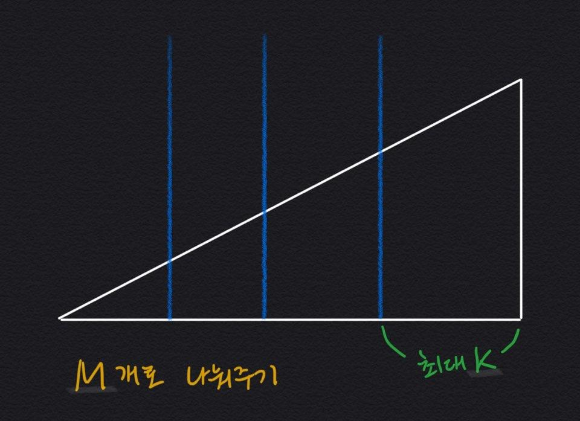

짠
각 그룹의 첫번째 요소들은 최대 부분 증가 수열이 된다.
M개의 그룹이므로 최대 부분 증가 수열의 개수가 M이 되어 문제 조건을 충족한다.
길이가 K인 그룹은 최대 부분 감소 수열이 된다.
그러기 위해서는 그룹 중 반드시 하나는 길이가 K여야 한다.
또한 그림에서 보이는 것처럼 두 부분 수열은 반드시 하나의 요소를 공유하게 된다.
이 조건은 불가능한 경우를 구분하는데 활용한다.
'Algorithm > BOJ' 카테고리의 다른 글
| [BOJ]11651번: 좌표 정렬하기 2 (c++) (0) | 2020.07.06 |
|---|---|
| [BOJ]2873번: 롤러코스터 (c++) (0) | 2020.06.27 |
| [BOJ]12904번: A와 B (c++) (0) | 2020.06.27 |
| [BOJ]12970번: AB (c++) (0) | 2020.06.27 |
| [BOJ]12919번: A와 B 2 (c++) (0) | 2020.06.26 |

댓글