https://www.acmicpc.net/problem/11054
11054번: 가장 긴 바이토닉 부분 수열
첫째 줄에 수열 A의 크기 N이 주어지고, 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ N ≤ 1,000, 1 ≤ Ai ≤ 1,000)
www.acmicpc.net
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
|
#include <iostream>
#include <vector>
using namespace std;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// 입력
int n;
cin >> n;
vector<int> input(n);
for (int i = 0; i < n; i++)
{
cin >> input[i];
}
/*
바이토닉 수열의 길이
= max(i번째까지 "앞"에서부터 증가하는 부분수열 길이
+ i번째까지 "뒤"에서부터 증가하는 부분수열 길이
- 1)
*/
// 앞에서부터 증가하는 부분수열의 길이 구하기
vector<int> icrs_backward(n, 1);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < i; j++)
{
if (input[j] < input[i] && icrs_backward[j] + 1 > icrs_backward[i])
{
icrs_backward[i] = icrs_backward[j] + 1;
}
}
}
// 뒤에서부터 증가하는 부분수열의 길이 구하기
vector<int> icrs_forward(n, 1);
for (int i = n - 1; i >= 0; i--)
{
for (int j = n - 1; j > i; j--)
{
if (input[i] > input[j] && icrs_forward[j] + 1 > icrs_forward[i])
{
icrs_forward[i] = icrs_forward[j] + 1;
}
}
}
// 최대값 출력
int max = 0;
for (int i = 0; i < n; i++)
{
if (max < icrs_backward[i] + icrs_forward[i] - 1)
{
max = icrs_backward[i] + icrs_forward[i] - 1;
}
}
cout << max;
return 0;
}
Colored by Color Scripter
|
문제가 어렵다 싶으면...
다시 천천히 문제를 보면서 핵심을 짚어내려고 노력하자.
아니면 빠르게 답안을 보자 ㅜㅜ
수열 S가 어떤 수 Sk를 기준으로 S1 < S2 < ... Sk-1 < Sk > Sk+1 > ... SN-1 > SN을 만족한다면, 그 수열을 바이토닉 수열이라고 한다.
문제에서 주어진 바이토닉 수열을 그림으로 표현하면 다음과 같다.

대충 길이배열을 2개 만들어야겠구나 하는 느낌이 온다.
하지만 이대로 구현하려면 골치가 아파진다.
앞에서부터 감소하는 수열을 만들어봤자, 의미가 없다.
내가 필요한건 저 정점 K에서부터 감소하는 수열의 길이이다.
그러니 생각을 다시 해서
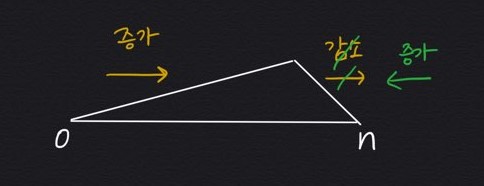
이렇게..
앞에서부터 증가하는 부분수열 길이배열 1개
뒤에서부터 증가하는 부분수열 길이배열 1개를 만들자.
그러면 icrs_forward[k] : k번째까지 뒤에서 부터 증가한 수열의 길이 이다.

즉, k번째 항을 꼭지점으로 하는 바이토닉 수열의 길이는 위와 같다.
이제 그중에서 max값만 계산하면 완성!
'Algorithm > BOJ' 카테고리의 다른 글
| [BOJ]2133번: 타일 채우기(c++) (0) | 2020.04.24 |
|---|---|
| [BOJ]13398번: 연속합 2(c++) (0) | 2020.04.23 |
| [BOJ]11722번: 가장 긴 감소하는 부분 수열(c++) (0) | 2020.04.23 |
| [BOJ]11055번: 가장 큰 증가 부분 수열(c++) (0) | 2020.04.23 |
| [BOJ]1932번: 정수 삼각형(c++) (0) | 2020.04.23 |

댓글